Задания «Сколько фигур»
встречались нам на подготовительных курсах в 1 класс и на олимпиадах по математике начальной школы для детей 6–8 лет. Они тренируют зрительно‑пространственный анализ, учат системно пересчитывать составные фигуры и формируют базовые навыки для геометрии. Данное пособие состоит из 3-х частей и направлено на развитие комбинаторного мышления, внимания.
Задания в этой части пособия могут звучать так:
- Найди все треугольники
- Сколько прямоугольников
- Сколько треугольников в каждой фигуре
- Сколько четрырехугольников на рисунке
- Сколько пятиугольников расположено на рисунке
Методические указания
При определении сколько фигур на рисунке основная задача — ВНИМАТЕЛЬНО перебрать ВСЕ ВАРИАНТЫ. На олимпиаде или тестированиях перебор осуществляется в уме. Для большинства детей — это сложная задача. Так как перебор происходит в произвольном порядке, то часть фигур остаются незамеченными и не посчитанными. Поэтому 1-ая часть пособия посвящена отработке алгоритма последовательного перебора.
Для этих целей подготовлены шаблоны для прорисовывания всех возможных вариантов в определенной последовательности.
Алгоритм перебора:
1) сначала ищем и считаем односоставные фигуры,
2) затем фигуры, состоящие из 2 фигур,
3) затем из 3-х и т.д.
На каждом шаге фигуры считаем по порядку — слева направо, сверху вниз или по кругу. Если замечаем, что ребенок начинает метаться, прыгать от односоставной фигуры к
сложносоставной, считать не по порядку, то возвращаем его к последовательному перебору.
Как решать на практике
-
Сделать «слои»: сначала отметить все минимальные треугольники, затем средние (из двух/трёх малых), затем самый большой.
-
Идти по опорным точкам: фиксировать одну вершину и перебирать варианты базовых сторон от неё.
-
Отмечать найденные треугольники точками/штрихами цветов, чтобы не считать дважды.
-
В конце перепроверить альтернативным способом (по размерам vs по вершинам) — результаты должны совпасть.
Таким образом во время работы над этими заданиями происходит тренировка произвольности — делать КАК НАДО, а не КАК ХОЧУ. Считать не все, что увиделось, а ПО ПОРЯДКУ.
Примеры олимпиадных задач типа «Сколько фигур»
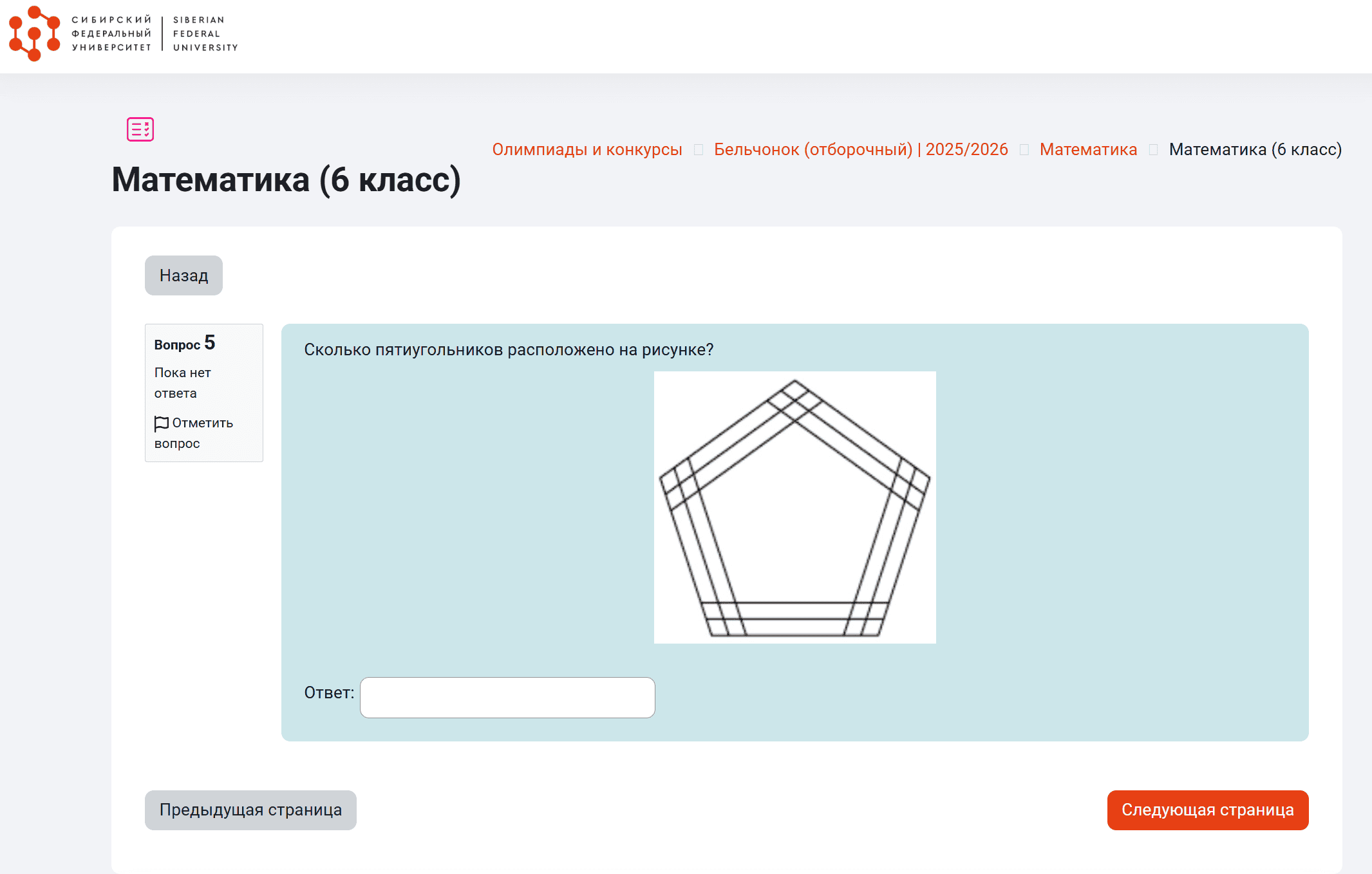
Олимпиада «Бельчонок», 2026, 6 класс.
Задача №5 — Сколько пятиугольников расположено на рисунке
Сразу после оплаты учебного пособия вам на почту придет ссылка на скачивание PDF-файла.